LA MAQUINA DE TURING

LA MÁQUINA DE TURING

Alan Mathison Turing, matemático y computador científico inglés, desarrolló entre 1935 y 1945 un modelo computacional hipotético que permitía en teoría resolver cualquier problema matemático siempre y cuando se reduzca a un algoritmo. 

imagen algoritmo

Una máquina de Turing es un dispositivo que manipula símbolos sobre una tira de cinta de acuerdo a una tabla de reglas.

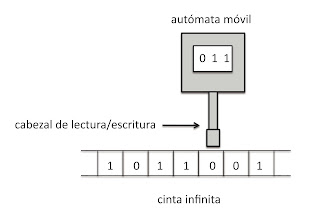
imagen maquina turing

Las máquinas de Turing ayudan a los científicos a entender los límites del cálculo mecánico. Turing dio una definición sucinta del experimento en su ensayo de 1948, «Máquinas inteligentes». Refiriéndose a su publicación de 1936, Turing escribió que la máquina de Turing, aquí llamada una máquina de computación lógica, consistía en:

...una ilimitada capacidad de memoria obtenida en la forma de una cinta infinita marcada con cuadrados, en cada uno de los cuales podría imprimirse un símbolo. En cualquier momento hay un símbolo en la máquina; llamado el símbolo leído. La máquina puede alterar el símbolo leído y su comportamiento está en parte determinado por ese símbolo, pero los símbolos en otros lugares de la cinta no afectan el comportamiento de la máquina. Sin embargo, la cinta se puede mover hacia adelante y hacia atrás a través de la máquina, siendo esto una de las operaciones elementales de la máquina. Por lo tanto cualquier símbolo en la cinta puede tener finalmente una oportunidad.2

Turing (1948, p. 61)

Los componentes de esta máquina son:

•   Memoria: se trata de una cinta ininitamente larga dividida en celdas cuadradas en cada una de las cuales hay un símbolo de un código(por ejemplo, un 1 o un 0, por lo que la cinta ocupa un bit). Este conjunto de símbolos o códigos es lo que se conoce como alfabeto de la máquina. En esta memoria se permite el almacenamiento tanto de la información introducida y de los datos de salida, como de los pasos intermedios que se han llevado a cabo para resolver el algoritmo, lo que permite hacer un seguimiento del proceso llevado a cabo. Debido al múltiple uso que se le da a la memoria y a la imposibilidad de conocer el número de pasos intermedios que la maquina va a necesitar, la cinta debe ser ilimitada. Es precisamente este detalle de memoria sin un lo que le otorga tanta importancia a la máquina de Turing.

•  Cabezal de lectura-escritura: es un dispositivo capaz de realizar cuatro operaciones: desplazarse una posición a la derecha respecto a la celda actual. desplazarse una posición a la izquierda, leer el contenido de la celda en la que se encuentra y escribir un símbolo distinto al que había sido leído por el cabezal o escribir nuevamente el que había en la celda.

•  Procesador: es un dispositivo digital que puede dividirse en dos partes atendiendo a las distintas funciones que cumple cada una dentro de la máquina:

• Por un lado. existe un registro de estado que contiene un número determinado de posibles estados internos de la máquina y que almacena el estado concreto en el que se encuentra el procesador.

•  Por otro lado. existe una tabla de acción que contiene las instrucciones de lo que realiza la máquina en cada instante de tiempo. Esta última parte del procesador es la encargada de decidir cuál será el nuevo estado, el simbolo que se va a escribir en la cinta y la dirección que tomará el cabezal dependiendo del carácter que se acaba de leer y del estado actual interno (es decir, esta parte contendría todo el programa posible de la máquina).

Con este aparato extremadamente sencillo es posible realizar cualquier cómputo que un computador digital sea capaz de realizar. 

Mediante este modelo teórico y el análisis de complejidad de algoritmos, fue posible la categorización de problemas computacionales de acuerdo a su comportamiento, apareciendo así, el conjunto de problemas denominados P y NP, cuyas soluciones en tiempo polinómico son encontradas según el determinismo y no determinismo respectivamente de la máquina de Turing. 

De hecho, se puede probar matemáticamente que para cualquier programa de computadora es posible crear una máquina de Turing equivalente. Esta prueba resulta de la Tesis de Church-Turing, formulada por Alan Turing y Alonzo Church, de forma independiente a mediados del siglo XX. 

Éste aparato tan sencillo tiene una propiedad sorprendente, y es que es capaz de implemetar cualquier problema matemático que se nos ocurra, con la única condición de que éste se pueda expresar por medio de un algoritmo (que recordemos que no es más que estructurar el problema en un número de pasos determinados) Por tanto, podremos escribir una cadena de símbolos que represente el problema de manera que la máquina lo pueda leer y, como además también puede escribir y borrar, cuando vayamos de un paso a otro del algoritmo podrá recordar el paso en el que se encuentra en cada momento para así poder dar el siguiente en la dirección correcta. Si nos fijamos bien, es sencillo encontrar una analogía entre una Máquina de Turing y un computador moderno. Ahora sí es fácil ver las implicaciones que el estudio teórico de la Máquina de Turing tiene en el avance de la Informática, pues nos permite, entre otras cosas, comprender los límites de lo que podemos esperar que haga una computadora y lo que no. Lo más curioso de todo esto es que, en realidad, cuando Alan Turing descubrió su máquina no lo hizo buscando la forma de inventar un ordenador personal (al menos no era su principal motivación), sino tratando de resolver el Problema de la decisión.

Alan Turing probó que cualquier método de implemetar un problema se puede siempre simplificar a una Máquina de Turing, es decir, que su máquina era algo así como “la madre de todos los métodos”. Por otro lado, también probó que no se puede construir una Máquina de Turing capaz de determinar si un problema se va a poder resolver o no y, por tanto, quedó demostrado que no hay ningún sistema para decidir si un problema matemático tiene solución o no, ya que si lo hubiera, nos encontraríamos con la paradoja de que el sistema se podría reducir a una Máquina de Turing que sabemos a ciencia cierta que no existe.